다익스트라 알고리즘: 다익스트라(데이크스트라)가 만든 알고리즘. https://ko.wikipedia.org/wiki/에츠허르_데이크스트라

1. 출발지를 s로 정하고, 다음과 같이 표시한다.
(s, t, x, y, z 순)
거리 = [0, inf, inf, inf, inf]
방문 = [True, False, False, False, False]
2. 갈 수 있는 노드들의 최소거리를 측정한다.
s->t: 10
s->y: 5
(s, t, x, y, z 순)
거리 = [0, 10, inf, 5, inf]
방문 = [True, False, False, False, False]
3. 방문 안한 녀석들 중 가장 가까운 녀석인 y를 방문하고, 최소거리를 측정한다.
(이미 값이 있으면 업데이트)
y->t: 3
y->x: 9
y->z: 2
(s, t, x, y, z 순)
거리 = [0, 8, 14, 5, 7]
방문 = [True, False, False, True, False]
4. 방문 안한 녀석들 중 가장 가까운 녀석인 z를 방문하고, 최소거리를 측정한다.
z->x: 6
(s, t, x, y, z 순)
거리 = [0, 8, 13, 5, 7]
방문 = [True, False, False, True, True]
5. 방문 안한 녀석들 중 가장 가까운 녀석인 t를 방문하고, 최소거리를 측정한다.
t->x: 1
t->y: 2
(s, t, x, y, z 순)
거리 = [0, 8, 9, 5, 7]
방문 = [True, True, False, True, True]
6. 방문 안한 녀석들 중 가장 가까운 녀석인 x를 방문하고, 최소거리를 측정한다.
x->z: 4
(s, t, x, y, z 순)
거리 = [0, 8, 9, 5, 7]
방문 = [True, True, True, True, True]
7. 방문 안한 노드가 없으므로 끝낸다.
(s, t, x, y, z 순)
거리 = [0, 8, 9, 5, 7]
방문 = [True, True, True, True, True]
다익스트라 코드구현(naive, heapq)
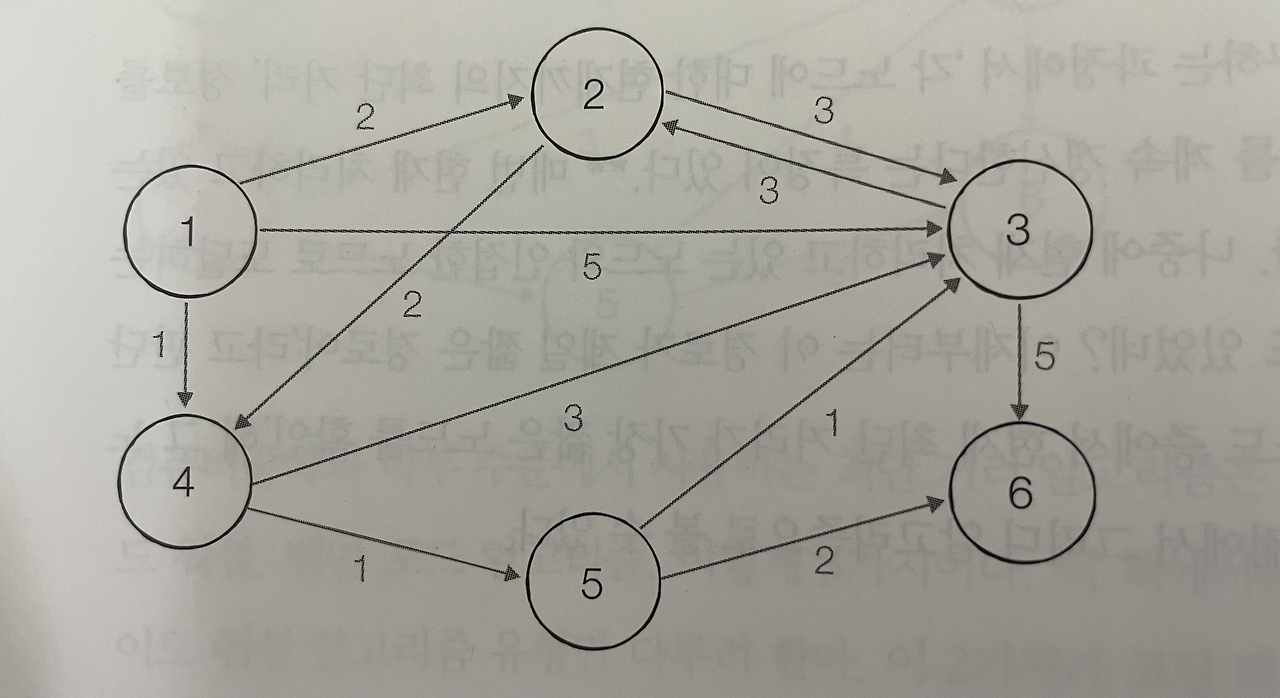
위와 같은 그래프가 있을 때

위와 같은 정답이 나오도록 하는 코드:
- 입력 코드
6 11
1
1 2 2
1 3 5
1 4 1
2 3 3
2 4 2
3 2 3
3 6 5
4 3 3
4 5 1
5 3 1
5 6 2-실행 코드
import sys
from min_cost.dijkstra import dijkstra_naive, dijkstra_pq
# testcase1.txt파일을 f라는 이름으로 염.(위에 입력코드)
with open('testcase1.txt') as f:
sys.stdin = f
# 한 줄씩 input에 저장
input = sys.stdin.readline
n, m = map(int, input().split())
start = int(input())
# 그래프 생성 및 삽입. 첫번째는 비워둠
graph = [[] for _ in range(n + 1)]
for _ in range(m):
a, b, c = map(int, input().split())
graph[a].append((b, c))
assert dijkstra_naive(graph, start) == [1000000000, 0, 2, 3, 1, 2, 4]
assert dijkstra_pq(graph, start) == [1000000000, 0, 2, 3, 1, 2, 4]-다익스트라 알고리즘 구현 코드(naive)
INF = int(1e9) #10억
# 시간복잡도 O(V^2)
def dijkstra_naive(graph, start):
# 방문할 가장 작은 비용의 노드 고르는 함수
def get_smallest_node():
min_value = INF
idx = 0
방문배열과 거리배열을 돌면서 총 코스트와 인덱스를 반환
for i in range(1, N):
if dist[i] < min_value and not visited[i]:
min_value = dist[i]
idx = i
return idx
N = len(graph)
# 그래프 노드만큼 방문배열과 길이배열 생성
visited = [False] * N
dist = [INF] * N
# 시작노드 설정
visited[start] = True
dist[start] = 0
# 시작노드에서 거리 추정
for adj, d in graph[start]:
dist[adj] = d
# N개의 노드 중 첫 노드는 이미 방문했으므로,
# N-1번 수행하면 된다.
for _ in range(N - 1):
# 가장 가깝고 방문 안한 녀석을 고르고,
cur = get_smallest_node()
visited[cur] = True
# 최단거리를 비교, 수정한다.
for adj, d in graph[cur]:
cost = dist[cur] + d
if cost < dist[adj]:
dist[adj] = cost
return dist
-다익스트라 알고리즘 구현 코드(heapq)
import heapq
# 우선순위 큐라는 개념을 최소 힙을 사용해서 구현한 코드
# 시간복잡도 O(ElogV)
def dijkstra_pq(graph, start):
N = len(graph)
dist = [INF] * N
#방문 배열 필요없음
q = []
# 튜플일 경우 0번째 요소 기준으로 최소 힙 구조.
# 첫 번째 방문 누적 비용은 0이다.
# heapq는 생성된 배열을 가지고 만듦
heapq.heappush(q, (0, start))
dist[start] = 0
while q:
# 누적 비용이 가장 작은 녀석을 꺼낸다.
acc, cur = heapq.heappop(q)
# 이미 답이 될 가망이 없다. (이미 방문한 노드)
if dist[cur] < acc:
continue
# 인접 노드를 차례대로 살펴보며 거리를 업데이트한다.
for adj, d in graph[cur]:
cost = acc + d
if cost < dist[adj]:
dist[adj] = cost
heapq.heappush(q, (cost, adj))
return dist'알고리즘' 카테고리의 다른 글
| 모듈러 산술 연산의 이해. (0) | 2024.07.18 |
|---|---|
| N-Queen 문제와 백 트래킹 (0) | 2024.07.17 |
| 94. 타겟 넘버(재귀를 통한 DFS) (2) | 2024.07.17 |
| 에라토스테네스의 체 (0) | 2024.07.09 |
| 유클리드 호제법 (약수 개수, 최대 공약수, 최소 공배수) (0) | 2024.07.09 |