1. N-Queen 문제란? (link)
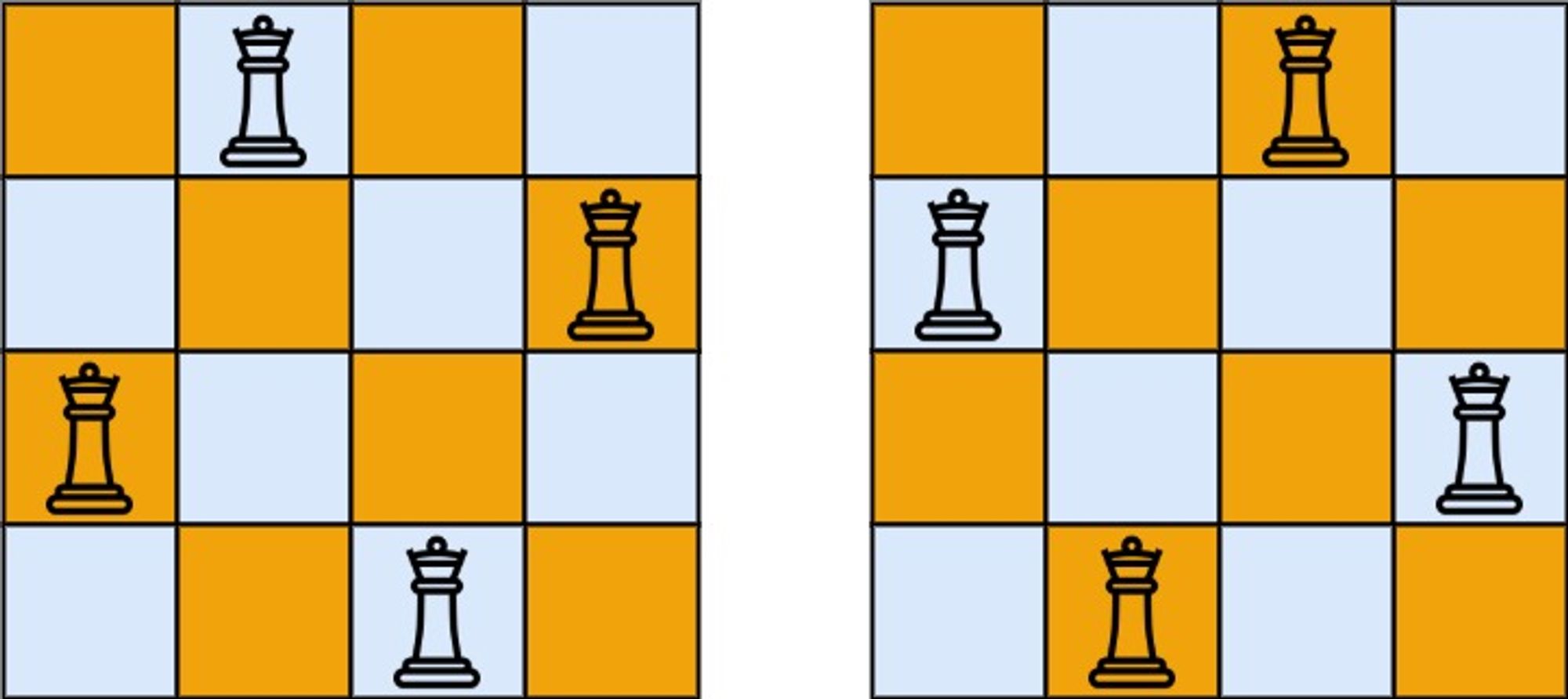
- N*N 체스판에 N개의 퀸을 배치할 수 있는 경우의 수를 센다.
- 퀸은 상하좌우, 대각선 방향으로 거리 제한 없이 이동할 수 있다.
- N=8인 경우, 경우의 수는 다음과 같다.
- 64 * 63 * ... * 57 = 178,462,987,637,760
- C 기준 1초에 1억 번을 연산하므로 모든 경우의 수를 탐색하는데 약 20.6시간이 소요된다.
2. 백 트래킹
- 필요없는 경우를 가지치기(pruning)함으로써 시간복잡도를 줄이는 방법을 백트래킹이라고 한다.

파이썬 코드:
def nqueen(n):
"""
visited 의 인덱스는 행, 값은 열을 나타낸다.
(1, 3)에 놓은 경우, visited[1] = 3 으로 표현하겠다는 것.
예시) n=4 이고 visited = [1, 3, 0, 2] 인 경우,
체스판을 그려보면 아래와 같다. (1이 퀸)
0 1 0 0
0 0 0 1
1 0 0 0
0 0 1 0
"""
visited = [-1] * n
cnt = 0
answers = []
def is_ok_on(nth_row):
"""
n번째(nth) 행에 퀸을 놓았을 때, 올바른 수인지 검사한다.
nth 행의 퀸 위치와, 0번째 행부터 n-1번째 행까지 놓여진 퀸의 위치를 비교한다.
nth 행에 놓여진 퀸이 규칙을 깼다면 False 를 반환한다.
"""
# 0번째 행 ~ nth_row-1번째 행의 퀸 위치를 차례대로 꺼내온다.
# 영상에서 n-1이라고 말하는데 오류입니다. nth_row-1까지 살펴봅니다.
for row in range(nth_row):
# 방금 놓여진 nth 퀸은 (nth_row, visited[nth_row]) 에 놓여져있다.
# 각 행에 차례대로 단 한 번만 두기 때문에 행이 겹치는 것은 검사하지 않아도 된다.
# 1) 열 번호가 겹치지는 않는지? visited[nth_row] == visited[row]:
# 2) 또는 대각선으로 존재하지는 않는지? nth_row - row == abs(visited[nth_row] - visited[row]) 살펴본다.
if visited[nth_row] == visited[row] or nth_row - row == abs(visited[nth_row] - visited[row]):
return False
return True
def dfs(row):
"""
row 는 퀸을 놓을 행번호를 의미한다.
dfs(0) 은 0번째 행에서 퀸의 위치를 고르는 것이고,
dfs(1) 은 1번째 행에서 퀸의 위치를 고르는 것이고,
...
dfs(n-1) 은 n-1번째 행에서 퀸의 위치를 고르는 것이다.
따라서 row 는 n-1까지 가능하며, n이 되었다는 것은 n개의 퀸을 모두 올바른 위치에 두었다는 의미이다.
"""
# 0 ~ n-1 행에 퀸을 모두 하나씩 두었을 때 경우의 수를 1 증가시키고 재귀탐색을 종료한다.
if row >= n:
# nonlocal 은 지역변수가 아님을 의미한다.
nonlocal cnt
cnt += 1
print("*" * 80)
print(f"{cnt}번째 답 - visited: {visited}")
grid = [['.'] * n for _ in range(n)]
for idx, value in enumerate(visited):
grid[idx][value] = 'Q'
result = []
for row in grid:
print(row)
result.append(''.join(row))
answers.append(result)
################
return
# visited[row] 의 값을 결정한다.
# n*n 의 체스판이므로 가능한 열의 범위는 0 ~ n-1 이다.
for col in range(n):
# (row, col) 위치에 퀸을 두었다고 가정하고, 규칙을 깨지 않는다면 row+1 행에 다시 퀸을 둔다.
visited[row] = col
if is_ok_on(row):
dfs(row + 1)
# 0번째 행에 퀸을 둔다.
dfs(0)
return answers
assert nqueen(4) == [[".Q..", "...Q", "Q...", "..Q."], ["..Q.", "Q...", "...Q", ".Q.."]]
'알고리즘' 카테고리의 다른 글
| 다익스트라 알고리즘 (2) | 2024.07.24 |
|---|---|
| 모듈러 산술 연산의 이해. (0) | 2024.07.18 |
| 94. 타겟 넘버(재귀를 통한 DFS) (2) | 2024.07.17 |
| 에라토스테네스의 체 (0) | 2024.07.09 |
| 유클리드 호제법 (약수 개수, 최대 공약수, 최소 공배수) (0) | 2024.07.09 |