1. 버블 정렬(이전 글)
2. 선택 정렬 (이전 글)
3. 삽입 정렬 (이전 글)
4. 퀵 정렬 (이전 글)
5. 합병 정렬
6. 힙 정렬
5. 합병 정렬(Merge Sort): 데이터를 낱개로 쪼갠 후 merge 함수를 이용해 병합하는 방식


5-1 merge함수: 두 정렬된 파일을 하나의 파일로 합쳐 빈 파일에 저장하는 함수
A= [1, 2, 3, 5] # 정렬된 배열 A
B= [4, 6, 7, 8] # 정렬된 배열 B
C= [] # 두 집합을 합칠 빈 배열 C
↓
1단계 : [1, 2, 3, 5]
↓
[4, 6, 7, 8]
1과 4를 비교합니다!
1 < 4 이므로 1을 C 에 넣습니다.
C:[1]
↓
2단계 : [1, 2, 3, 5]
↓
[4, 6, 7, 8]
2와 4를 비교합니다!
2 < 4 이므로 2를 C 에 넣습니다.
C:[1, 2]
↓
3단계 : [1, 2, 3, 5]
↓
[4, 6, 7, 8]
3과 4를 비교합니다!
3 < 4 이므로 3을 C 에 넣습니다.
C:[1, 2, 3]
↓
3단계 : [1, 2, 3, 5]
↓
[4, 6, 7, 8]
5와 4를 비교합니다!
5 > 4 이므로 4을 C 에 넣습니다.
C:[1, 2, 3, 4]
↓
3단계 : [1, 2, 3, 5]
↓
[4, 6, 7, 8]
5와 6을 비교합니다!
5 < 6 이므로 5을 C 에 넣습니다.
C:[1, 2, 3, 4, 5]
A 의 모든 원소 삽입 끝났습니다.
이후, B에서 안 들어간 원소인
[6, 7, 8] 하나씩 C 에 추가해주면 됩니다.
C:[1, 2, 3, 4, 5, 6, 7, 8]
그러면 A 와 B를 합치면서 정렬할 수 있었습니다.
merge함수 구현 코드
#두 정렬된 배열을 받고
def merge(arr1, arr2):
#새 배열에 정렬해서 리턴
result = []
i = j = 0
#두 배열 비교하면서 작은거 먼저 result에 append한 후 다음 요소로 넘김
while i < len(arr1) and j < len(arr2):
if arr1[i] < arr2[j]:
result.append(arr1[i])
i += 1
else:
result.append(arr2[j])
j += 1
#요소 끝까지 비교 안했으면 나머지 넣음(어차피 정렬된 배열이라 append만 하면 됨)
while i < len(arr1):
result.append(arr1[i])
i += 1
#마찬가지
while j < len(arr2):
result.append(arr2[j])
j += 1
return result
5-2 merge함수를 이용한 Merge Sort
def mergesort(lst):
#데이터를 낱개로 나눠버리면 정렬할것도 없이 하나라 이미 정렬되어있다고 간주
if len(lst) <= 1:
return lst
mid = len(lst) // 2
#가운데를 기준으로 왼쪽과 오른쪽 정렬하기
L = lst[:mid]
R = lst[mid:]
return merge(mergesort(L), mergesort(R))
5-3 합병 정렬시간 복잡도:

[1, 2, 3, 4, 5, 6, 7, 8] 을 정렬하기 위해
[1, 2, 3, 5] 과 [4, 6, 7, 8] 을 병합했습니다.
[1, 2, 3, 5] 과 [4, 6, 7, 8] 을 정렬하기 위해
[3, 5] [1, 2] 과 [6, 8] [4,7] 을 병합했습니다.
[3, 5] [1, 2] 과 [6, 8] [4,7] 을 정렬하기 위해
[5] [3] [2] [1] [6] [8] [7] [4] 를 병합했습니다.
이를 얼마나 시간이 걸리는지에 대한 관점으로 보면,
T(N) 을 N 의 길이를 정렬하기 위해 걸리는 시간이라고 하겠습니다.
1단계
[1, 2, 3, 4, 5, 6, 7, 8] 을 정렬하기 위해
[1, 2, 3, 5] 과 [4, 6, 7, 8] 을 병합했습니다.
즉, 크기 N 인 배열을 정렬하기 위해
크기 N/2 인 부분 배열 2개를 비교 합니다.
그러면 N/2 * 2 = N 번 비교하게 됩니다
2단계
[1, 2, 3, 5] 과 [4, 6, 7, 8] 을 정렬하기 위해
[3, 5] [1, 2] 과 [6, 8] [4,7] 을 병합했습니다.
즉, 크기 N/2 인 부분 배열 2개를 정렬하기 위해
크기 N/4 인 부분 배열 4개를 비교 합니다.
그러면 N/4 * 4 = N 번 비교하게 됩니다
3단계
[3, 5] [1, 2] 과 [6, 8] [4,7] 을 정렬하기 위해
[5] [3] [2] [1] [6] [8] [7] [4] 를 병합했습니다.
즉, 크기 N/4 인 부분 배열 4개를 정렬하기 위해
크기 N/8 인 부분 배열 8개를 비교 합니다.
그러면 N/8 * 2 = N 번 비교하게 됩니다
즉 모든 단계에서 N 만큼 비교를 합니다.
그러면 총 몇 단계인지만 알면 시간 복잡도를 구할 수 있습니다!
크기가 N → N/2 → N/2^2 → N/2^3 → .... → 1
등비수열의 합으로 인해 k = log_2N
바로 log_2N 번 반복하게 되면 1이 됩니다.
이걸 수식으로 나타내면
N만큼의 연산을 logN 번 반복한다고 해서
시간 복잡도는 총 O(Nlog_2N) = O(NlogN) 이 된다! 라고 생각할 수 있습니다.
6. 힙 정렬(Heap Sort): 힙으로 정렬하는 방법
6-1 힙(Heap): 힙은 데이터에서 최대값과 최소값을 빠르게 찾기 위해 고안된 완전 이진 트리(Complete Binary Tree)
8 Level 0
6 3 Level 1
2 1 Level 2 # -> 이진 트리 O 완전 이진 트리 X 이므로 힙이 아닙니다!
8 Level 0
6 3 Level 1 # -> 이진 트리 O 완전 이진 트리 O 인데 모든 부모 노드의 값이
4 2 Level 2 # 자식 노드보다 크니까 힙이 맞습니다!
8 Level 0
6 3 Level 1 # -> 이진 트리 O 완전 이진 트리 O 인데 모든 부모 노드의 값이
4 2 5 Level 2 # 자식 노드보다 크진 않아서 힙이 아닙니다..!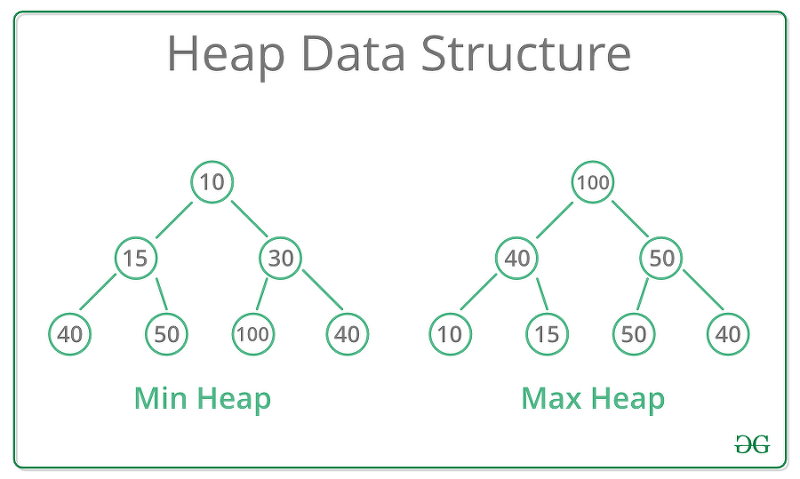
- BST(이진탐색트리)와 다르다. 좌, 우 자식의 위치가 대소관계를 반영하지 않음. (
그림 참조) - 계산 편의를 위해 인덱스는 1부터 사용한다. (parent: x, left: 2x, right: 2x+1)
6-2 최소 힙 - 삽입 시간복잡도와 추출 시간복잡도
원소를 삽입할 때는결국 원소를 맨 밑에 넣어서 꼭대기까지 비교하면서 올리고 있습니다.
완전 이진트리의 최대 높이는 O(log(N))
그러면, 반복하는 최대 횟수도 O(log(N)) 입니다.
즉! 최소 힙의 원소 추가는 (log(N)) 만큼의 시간 복잡도를 가진다고 분석할 수 있습니다.
마찬가지로 원소를 추출할때도 (log(N)) 만큼의 시간 복잡도를 가진다고 분석할 수 있습니다.
힙 정렬(Heap Sort)는 삽입하는 노드가 총 n개이므로 평균과 최악 모두 시간복잡도는 O(nlogn) 입니다.
힙 코드 구현
class BinaryMinHeap:
def __init__(self):
# 계산 편의를 위해 0이 아닌 1번째 인덱스부터 사용한다.
self.items = [None]
def __len__(self):
# len() 연산을 가능하게 하는 매직 메서드 덮어쓰기(Override).
return len(self.items) - 1
#들어온 노드 루트노드로 보내는 함수
def _percolate_up(self):
# percolate: 스며들다.
cur = len(self)
# left 라면 2*cur, right 라면 2*cur + 1 이므로 parent 는 항상 cur // 2
parent = cur // 2
while parent > 0:
if self.items[cur] < self.items[parent]:
self.items[cur], self.items[parent] = self.items[parent], self.items[cur]
cur = parent
parent = cur // 2
#힙 트리 유지시키는 함수
def _percolate_down(self, cur):
smallest = cur
left = 2 * cur
right = 2 * cur + 1
if left <= len(self) and self.items[left] < self.items[smallest]:
smallest = left
if right <= len(self) and self.items[right] < self.items[smallest]:
smallest = right
#왼쪽이든 오른쪽이든 자식노드가 부모노드보다 작다면 스위치
if smallest != cur:
self.items[cur], self.items[smallest] = self.items[smallest], self.items[cur]
#반복
self._percolate_down(smallest)
#노드 넣는 함수
def insert(self, k):
self.items.append(k)
self._percolate_up()
#제일 작은 값 추출 (부모노드)
def extract(self):
if len(self) < 1:
return None
root = self.items[1]
self.items[1] = self.items[-1]
self.items.pop()
self._percolate_down(1)
return root
6-3 힙 정렬 코드구현(위에 힙 코드가 포함되어 있어야함)
def heapsort(lst):
#최소 힙 인스턴스 만들고
minheap = BinaryMinHeap()
#요소들 다 넣어준 다음
for elem in lst:
minheap.insert(elem)
#extract하면 항상 루트노드에 최솟값이 들어가기 때문에 뽑은것들 계속 result에 append하면 됨
return [minheap.extract() for _ in range(len(lst))]
'알고리즘' 카테고리의 다른 글
| 에라토스테네스의 체 (0) | 2024.07.09 |
|---|---|
| 유클리드 호제법 (약수 개수, 최대 공약수, 최소 공배수) (0) | 2024.07.09 |
| 알고리즘 3 (버블 정렬, 선택 정렬, 삽입 정렬, 퀵 정렬) (0) | 2024.06.27 |
| 파이썬 미로 탈출 경로 찾기 / 순열 생성하기 (0) | 2024.06.20 |
| 알고리즘 2 (BFS, 백 트래킹, 이진탐색) (1) | 2024.06.17 |